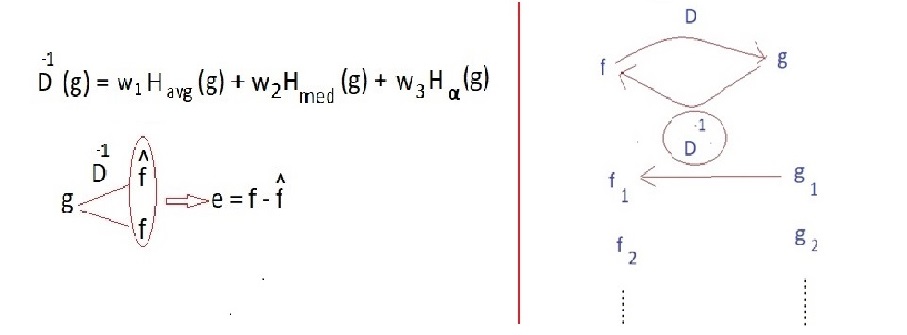اصلاح تصویر و حذف نویز در متلب 2

تابع Wiener  و روش آماری فیلتر NSPR در متلب

 

آموزش برنامه نویسی در متلب12

 نوشته ها :

1-  حذف نویز با فیلترهای مکان 

2- تابع Wiener Filtering

3- روش آماری فیلتر NSPR  

4- تخمین زدن با روش آماری واریانس 

5- تابع deconvwnr

6- فراخوانی به روش J = deconvwnr ( I , PSF , NSR ) 

7- فرا خوانی به روش J = deconvwnr ( I , PSF , NCORR , ICORR )  

 

چگونگی اصلاح تصویر و حذف نویز و تابع Wiener Filtering و روش آماری فیلتر NSPR در متلب را بررسی میکنیم .

 حذف نویز با فیلترهای مکان :

با افزودن نویز به خانواده ای از تصاویر میتوانیم با ایجاد یک سیستم فازی با کمترین خطا تصویر را بهبود دهیم در این فیلتر ها تصویر ورودی نویز دار و خروجی تصویر اصلی است .

 

با شناختن پایه های فیلترینگ به ترکیب آن می پردازیم .

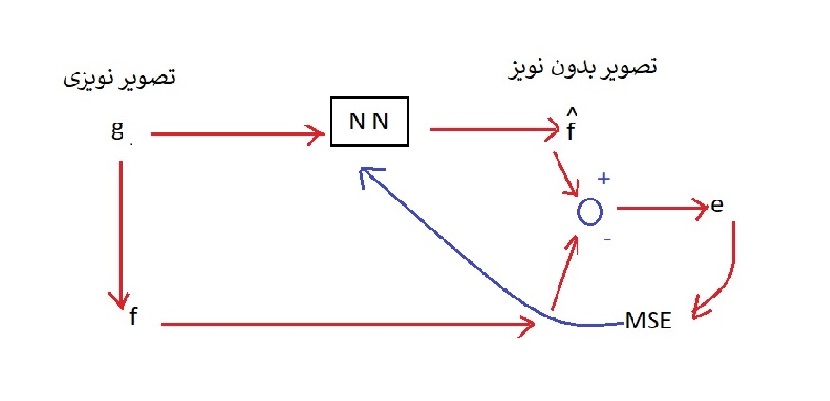
پایه عملکرد را MSE قرار میدهیم و با توجه به آن ساختار عصبی شبکه را تغییر میدهیم .

این روش نتیجه مطلوبی در حذف نویزها ندارد .

به بررسی روش های قوی تری در باز سازی تصویر در حوزه فرکانس میپردازیم .

تصویر ورودی متفاوت تغییرات متفاوتی را به همراه دارد .

یکی از راه ها Wiener Filtering است .

با Wiener Filtering  به کمترین خطا میرسیم .

چون تابع هدف( E )در مکان راحت به نتیجه نمیرسد حل آن را در حوزه فرکانس انجام میدهیم .

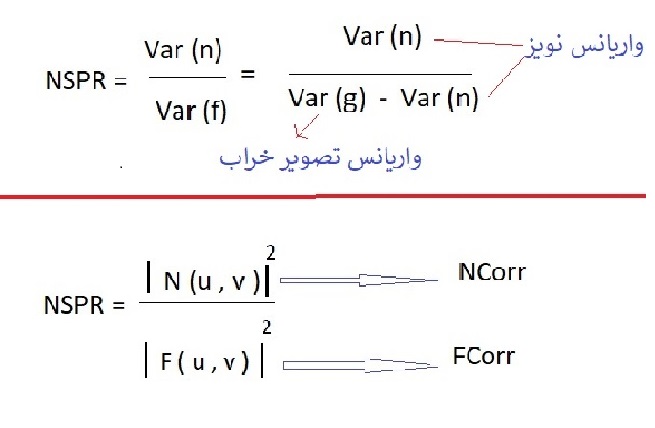
  F  درNSPR  مجهول است برای یافتن آن فرمول را به توابعی که داریم تبدیل میکنیم تا شدت نسبی را بیابیم .

برای نمایش  NSPR ثابت نماد خط بالای آن را بر میداریم .

این مدل  NSPR از دید آمار میگوید .

PSF ماتریس وزنی تبدیل مکانی است .

 میزان نویز به سیگنال را NSR نمایش میدهد .

رابطه نویز را با نویز NCORR .

رابطه تصویر با تصویرICORR .

بررسی حذف نویز :

 

1. Clc ;
   Clear ;
   Close all ;
   % % Read Image
   f =imread ( ‘ Cameraman . tif ‘ ) ;
   f = im2double (f) ;
   % % Apply Motion Filter
   MotionLength = 7 ;
   MotionAngle = 45 ;
   PSF = fspecial ( ‘ motion ‘ , MotionLength , MotionAngle ) ;
   g1 = imfilter ( f , PSF) ;
   % % Add Noise
   NoiseMean = 0 ;
   NoiseVar = 0 . 01 ;
   g2 = imnoise ( g1 , ‘gaussian ‘ , NoiseMean , NoiseVar ) ;
   % % Wiener Deconvolution
   
   % % Results
   figure ;
   subplot ( 2 , 2 , 1 ) ;
   imshow ( f ) ;
   title ( ‘ Original Image ‘ ) ;
   subplot ( 2 , 2 , 2 ) ;
   imshow ( g1) ;
   title ( ‘ Blurred Image ‘ ) ;
   subplot ( 2 , 2 , 3) ;
   imshow ( g2) ;
   title ( ‘ Blurred and Noisey Image ‘ ) ;

 

 با دستور  J = deconvwnr ( I , PSF , NSR )  تصویری با 45 درجه چرخش رابا فرض داشتن PSF بازیابی و نویز را حذف میکنیم .

بررسی با روش آماری واریانس :

1. % % Wiener Deconvolution
   % ImageVar = Var (f(:)) ;
   % NSPR = NoiseVar ;
   Fhat 1 = deconvwnr (g2 , PSF , 0 ) ;
   % % Results
   figure ;
   subplot ( 2 , 3 , 1 ) ;
   imshow ( f ) ;
   title ( ‘ Original Image ‘ ) ;
   subplot ( 2 , 3 , 2 ) ;
   imshow ( g1) ;
   title ( ‘ Blurred Image ‘ ) ;
   subplot ( 2 , 3 , 3) ;
   imshow ( g2) ;
   title ( ‘ Blurred and Noisey Image ‘ ) ;
   subplot ( 2 , 3 , 4) ;
   imshow ( fhat1 ) ;
   title ( ‘ Recovered Image ( NPSR = 0 ) ‘ ) ;

 

بدون نویز کارایی ندارد چون تصویر مخدوش میشود .

از NSPR استفاده میکنیم .

 

1. % % Add Noise
   NoiseMean = 0 ;
   NoiseVar = 0 . 001 ;
   g2 = imnoise ( g1 , ‘gaussian ‘ , NoiseMean , NoiseVar ) ;
   % % Wiener Deconvolution
   NSPR1 = 0 ;
   Fhat 1 = deconvwnr (g2 , PSF , NSPR1 ) ;
   ImageVar = Var (f (:) ) ;
   NSPR2 = NoiseVar / ImageVar ;
   Fhat2 = deconvwnr (g2 , PSF , NSPR2 ) ;
   % % Results
   figure ;
   subplot ( 2 , 3 , 1 ) ;
   imshow ( f ) ;
   title ( ‘ Original Image ‘ ) ;
   subplot ( 2 , 3 , 2 ) ;
   imshow ( g1) ;
   title ( ‘ Blurred Image ‘ ) ;
   subplot ( 2 , 3 , 3) ;
   imshow ( g2) ;
   title ( ‘ Blurred and Noisey Image ‘ ) ;
   subplot ( 2 , 3 , 4) ;
   imshow ( fhat1 ) ;
   title ( ‘ Recovered Image ( NPSR = 0 ) ‘ ) ;
   subplot ( 2 , 3 , 5) ;
   imshow ( fhat2 ) ;
   title ( [ ‘ Recovered Image ( NPSR = ‘ num2str ( NSPR2) ‘ ) ‘  ] ) ;

 

حرکت 45 درجه ای تصویر را با ده برابر کم کردن واریانس نویزی بی اثر کردیم و به وضوح تصویر اصلی رسیدیم حالا به برطرف کردن اثر نویز میپردازیم .

1. % % Wiener Deconvolution
   NSPR1 = 0 ;
   Fhat 1 = deconvwnr (g2 , PSF , NSPR1 ) ;
   ImageVar = Var (f (:) ) ;
   NSPR2 = NoiseVar / ImageVar ;
   Fhat2 = deconvwnr (g2 , PSF , NSPR2 ) ;
   NSPR3 = 0 .05 ;
   Fhat3 = deconvwnr (g2 , PSF , NSPR3 ) ;
   % % Results
   figure ;
   subplot ( 2 , 3 , 1 ) ;
   imshow ( f ) ;
   title ( ‘ Original Image ‘ ) ;
   subplot ( 2 , 3 , 2 ) ;
   imshow ( g1) ;
   title ( ‘ Blurred Image ‘ ) ;
   subplot ( 2 , 3 , 3) ;
   imshow ( g2) ;
   title ( ‘ Blurred and Noisey Image ‘ ) ;
   subplot ( 2 , 3 , 4) ;
   imshow ( fhat1 ) ;
   title ( ‘ Recovered Image ( NPSR = 0 ) ‘ ) ;
   subplot ( 2 , 3 , 5) ;
   imshow ( fhat2 ) ;
   title ( [ ‘ Recovered Image ( NPSR = ‘ num2str ( NSPR2) ‘ ) ‘  ] ) ;
   subplot ( 2 , 3 , 6) ;
   imshow ( fhat3 ) ;
   title ( [ ‘ Recovered Image ( NPSR = ‘ num2str ( NSPR3) ‘ ) ‘  ] ) ;

 

بیشتر نویزها حذف شد ولی تصویر تار شد .

اجرای فراخوانی با روش  J = deconvwnr ( I , PSF , NCORR , ICORR )  :

اول با پیدا کردن طیف نویز محاسبه میکنیم .

1. SN = abs (fft2 (g2 – g1)) . ^2 ;
   NCORR = fftshift (real (ifft2 (SN)) ;
   SF = abs (fft2(f)) . ^2 ;
   FCORR = fftshift (real (ifft2 (SF))) ;
   NSPR = NCORR . / FCORR ;
   Fhat3 = deconvwnr ( g2 , PSF , NCORR , FCORR ) ;

 

همبستگی سیگنال در نقاط مختلف تصویر متفاوت است حالت کُریلیشن با خود .

از نویز گیری برای شفاف سازی پلاک خودرو جهت پلاک خوان پارکینگ در نرم افزار پارکینگ و کنترل تردد خودرو استفاده میگردد.

وضوح تصویر بالا ست برای کم کردن نویز اطراف تصویر تابع J = edgetaper (I , PSF) وارد عمل میشود .

1. PSF2 = fspecial (‘gaussian ‘ , 60 , 10 ) ;
   Fhat4 = edgetaper (fhat3 , PSF2 ) ;

 

با این تابع نویز حواشی هم کم شد و بیشترین شباهت به تصویر اصلی را دارد .

تابع Wiener و فیلتر NSPR در متلب نتایج متنوعی در اختیار ما میگذارد .