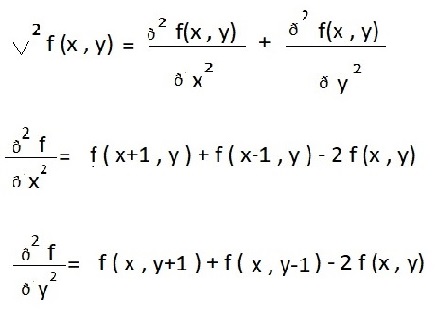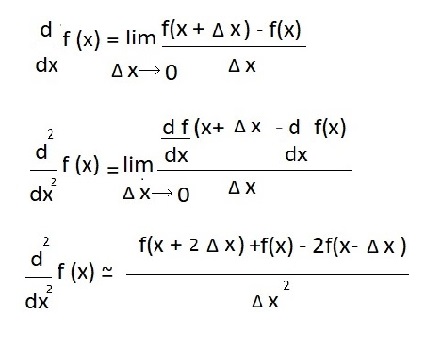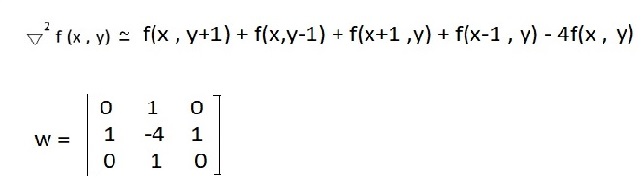spatial filtering روش های فیلترینگ مکانی متلب 2

توابع 2 Log – Laplacian – Ordfilt در متلب  

آموزش برنامه نویسی در متلب 6

 نوشته ها :

1- تابع Laplacian تقریبی از مشتق مرتبه 2

2- فرمول مشتق 

3- مشتق گیری دو بعدی 

4- فیلتر Log

5-  فیلتر sobel

6- فیلتر prewitt 

7- فیلترunsharp

8- کارکرد فیلتر های غیر خطی 

9- فیلتر Ordfilt 2

10- تابعMedfilt 2

در آموزش روش های فیلترینگ مکانی به توابع Log – Laplacian – Ordfilt , prewitt – sobel – unsharp در متلب میپردازیم .

 تابع Laplacian  تقریبی از مشتق مرتبه 2 است .

 

 

 

محاسبه تصویربا ماتریس مشتق مرتبه 2 معادل مشتق گیری دو بعدی

1. Clc;
   Clear ;
   Close all ;
   Img 0 = imread ( ‘ rice . png ‘ ) ;
   Alpha 1 = 0 ;
   W1 = fspecial ( ‘ laplacian ‘ , alpha 1 ) ;
   Img 1 = imfilter ( img 0 , w1 , ‘ circular ‘ ) ;
   Alpha 2 = 0 . 2 ;
   W2 = fspecial ( ‘ laplacian ‘ , alpha 2 ) ;
   Img 2 = imfilter ( img 0 , w2 , ‘ circular ‘ ) ;
   Alpha 3 = 0 . 4 ;
   W3 = fspecial ( ‘ laplacian ‘ , alpha 3 ) ;
   Img 3 = imfilter ( img 0 , w3 , ‘ circular ‘ ) ;
   Alpha 4 = 0  . 8 ;
   W4 = fspecial ( ‘ laplacian ‘ , alpha 4 ) ;
   Img 4 = imfilter ( img 0 , w4 , ‘ circular ‘ ) ;
   Alpha5= 1 ;
   W5 = fspecial ( ‘ laplacian ‘ , alpha 5 ) ;
   Img 5 = imfilter ( img 0 , w5 , ‘ circular ‘ ) ;
   Figure ;
   Subplot (2, 3 , 1 ) ;
   Imshow ( img 0 ) ;
   Title ( ‘ Original Image ‘ ) ;
   Subplot (2, 3 , 2 ) ;
   Imshow ( img 1 ) ;
   Title ( [ ‘ Laplacian with / alpha = num 2 str(alpha 1 ) ] ) ;
   Subplot (2, 3 ,3) ;
   Imshow ( img 2 ) ;
   Title ( [ ‘ Laplacian with \ alpha = num 2 str(alpha 2 ) ] ) ;
   Subplot (2, 3 , 4) ;
   Imshow ( img 3 ) ;
   Title ( [ ‘ Laplacian with\ alpha = num 2 str(alpha 3 ) ] ) ;
   Subplot (2, 3 , 5) ;
   Imshow ( img 4 ) ;
   Title ( [ ‘ Laplacian with \ alpha = num 2 str(alpha 4 ) ] ) ;
   Subplot (2, 3 ,6) ;
   Imshow ( img 5 ) ;
   Title ( [ ‘ Laplacian with\alpha = num 2 str(alpha5) ] ) ;
   
   
   
   

 همه تصاویر شبیه هم هستند و باعث شفاف سازی خطوط درجهات متفاوت هستند .

برای بهبود تصویر :

1. Functhon Xn = Normalize ( X , beta )

2. If nargin < 2
   Beta = 1 ;
   End
   X min = min ( x ( : ) ) ;
   X max = max ( x ( : ) ) ;
   XN = ( ( X – X min ) / ( X max – X min ) ) . ^ beta ;
   
   
   

با 1 گرفتن بتا حالت خطی ایجاد میشود وتصویر تغییری نمیکند ، بتا کمتر از 1 باشد تصویر یکنواخت میشود ، بتا بیشتر از 1 باشد فاصله بین سفید و سیاه بیشتر میشود .

 

فیلتر بالا گذر مشتق درجه 2 با مشتق عادی میتوانیم نقاط تغییر رنگ را نمایش دهیم .

اگر ضریبی از مشتق درجه 2 را به تصویر اصلی کم یا زیاد کنیم کیفیت تصویر بهبود میابد .

از پردازش تصویر در ساخت نرم افزار پلاک خوان جهت نرم افزار کنترل تردد خودرو و نیز نرم افزار پارکینگ استفاده میگردد. بیشتر استفاده آن در نرم افزار پارکینگ میباشد.

علامت عدد با w باید یکی باشد .

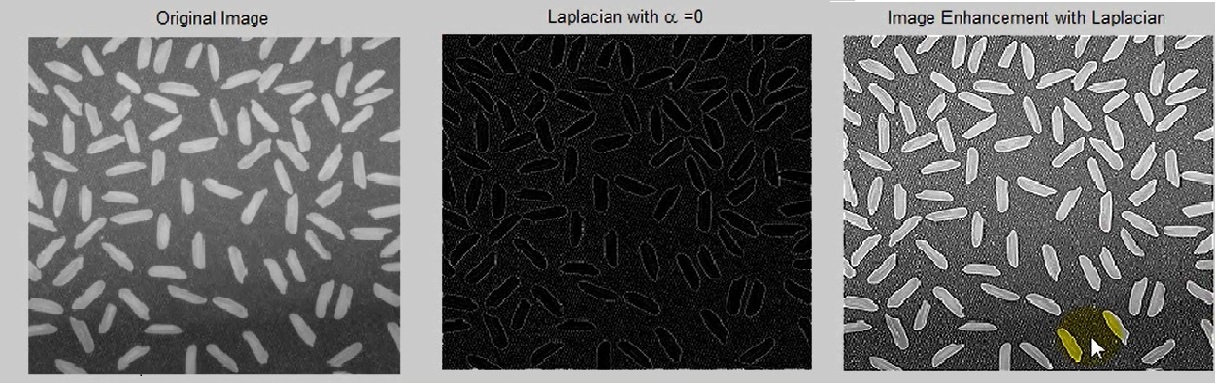
1. Clc;
   Clear ;
   Close all ;
   Img 0 = imread ( ‘ rice . png ‘ ) ;
   Img 0 = im2double ( img 0 ) ;
   Alpha  = 0 ;
   W = fspecial ( ‘ laplacian ‘ , alpha  ) ;
   Img 1 = imfilter ( img 0 , w , ‘ circular ‘ ) ;
   C = -1 ;
   Img 2 = img 0 + c * img 1 ;
   Figure ;
   Subplot ( 1 , 3 , 1 ) ;
   Imshow ( img 0 ) ;
   Title ( ‘ Original Image ‘ ) ;
   Subplot ( 1 , 3 , 2) ;
   Imshow ( img 1 ) ;
   Title ([ ‘ Laplacian with \ alpha = ‘ num2str ( alpha) ] ) ;
   Subplot ( 1 , 3 , 3 ) ;
   Imshow ( img 2 ) ;
   Title ( ‘ Image Enhancement with Laplacian ‘ ) ;

 

اگر فیلتر Laplacian را با تصویر اُرجینال جمع کنیم چنین نتیجه ای حاصل میشود .

Laplacian یک ترکیب خطی که با تصویر شبکه متوالی دارد وعلامت آن منفی است .

جاهایی که علامت مشتق تغییر کرده در تصویر نمایش میدهد .

تابع Log   :

در متلب از اِعمال تابع Laplacian بر فیلتر Gaussian ، تابع Log به دست می آید .

در برنامه نویسی متلب با دو آیکن Hsize , sigma سایز ماتریس را مینویسیم .

1. Clc;
   Clear ;
   Close all ;
   Img 1 = imread ( ‘ rice . png ‘ ) ;
   Sigma = 1 ;
   W = fspecial ( ‘ Log ‘ , 5 , sigma );
   >> w =  fspecial ( ‘ Log ‘ , 100 ) ;
   >> w = w / max ( w ( : ) ) ;
   >> imshow ( w )
   
   
   

 

1. >> w =  fspecial ( ‘ Log ‘ , 100 , 10 ) ;
   >> w = w / max ( w ( : ) ) ;
   >> imshow ( w )
   
   
   
   

 منفی بودن مرکز در محاسبات اثر گذار نیست .

1. >> w = Normalize ( w ) ;
   >> imshow ( w )

به شکل دایره های داخل هم نمایش داده شده که رنگ سفید مثبت رنگ خاکستری خنثی و رنگ سیاه منفی را میرساند .

برای بزرگ کردن حاشیه های تصویر مقصد استفاده از تابع log مفید است .

 درmotion حرکت لنز دوربین را با دو گزینه = طول حرکت را باLen  و زاویه حرکت را با theta نشان میدهیم

1. Clc;
   Clear ;
   Close all ;
   Img 0 = imread ( ‘ rice . png ‘ ) ;
   Img 0 = im2double ( img 0 ) ;
   W = fspecial ( ‘ motion ‘ , 40 , 45 ) ;
   Img = imfilter ( img 0 , w ,’circular ‘ ) ;
   Figure ;
   Subplot ( 1 , 2,1) ;
   Imshow ( img 0 ) ;
   Title ( ‘ Original Image ‘) ;
   Subplot ( 1 , 2,2) ;
   Imshow ( img 1 ) ;
   Title ( ‘ After Motion Filter ‘ ) ;

 

After Motion Filter یک فیلتر پایین گذر که کمی منحرف شده و جهت دارهم میباشد .

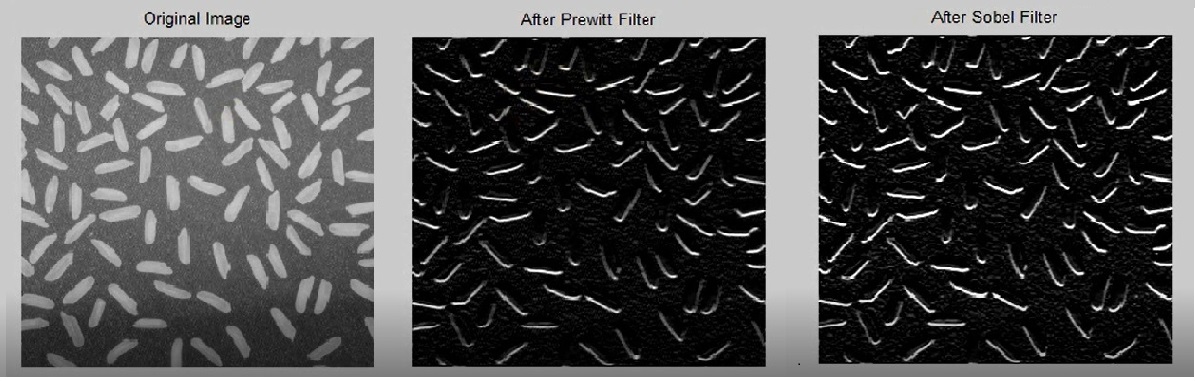
 برای تقویت حاشیه های تصویر از دو فیلتر مهم  prewitt , sobel در امتداد عمود یا افق استفاده میکنیم که تقریبی از مشتق دو بُعدی  یک تصویر میباشد .

1. >> w = fspecial ( ‘ prewitt ‘ )
   W =
   1 1 1
   0 0 0
   -1 -1 -1
   >> w = fspecial ( ‘ sobel ‘ )
   W =
   1 2 1
   0 0 0
   -1 -2 -1
   
   Clc;
   Clear ;
   Close all ;
   Img 0 = imread ( ‘ rice . png ‘ ) ;
   Img 0 = im2double ( img 0 ) ;
   Wp = fspecial ( ‘ prewitt ‘ ) ;
   Img 1= imfilter ( img 0 , wp ,’circular ‘ ) ;
   Ws = fspecial ( ‘ Sobel ‘ ) ;
   Img 2= imfilter ( img 0 , ws ,’circular ‘ ) ;
   Figure ;
   Subplot ( 1 , 3, 1) ;
   Imshow ( img 0 ) ;
   Title ( ‘ Original Image ‘) ;
   Subplot ( 1 , 3,2) ;
   Imshow ( img 1 ) ;
   Title ( ‘ After Prewitt Filter ‘ ) ;
   Subplot ( 1 , 3,3) ;
   Imshow ( img 2 ) ;
   Title ( ‘ After Sobel Filter ‘ ) ;

 

وقتی دستور برنامه مربوط به خطوط افقی باشد طبیعتا در نمایش خطهای افقی را بیشتر نمایش میدهد .

1. Clc;
   Clear ;
   Close all ;
   Img 0 = imread ( ‘ rice . png ‘ ) ;
   Img 0 = im2double ( img 0 ) ;
   Wp = fspecial ( ‘ prewitt ‘ ) ;
   Img 1= imfilter ( img 0 , wp ,’circular ‘ ) ;
   Img 2= imfilter ( img 0 , wp ,’circular ‘ ) ;
   Alpha = 0 . 3 ;
   Img 3= imfilter ( img 0 , alpha *wp + ( 1 – alpha ) * wp ‘ , ‘circular ‘ ) ;
   Ws = fspecial ( ‘ Sobel ‘ ) ;
   Img 4= imfilter ( img 0 , ws ,’circular ‘ ) ;
   Img 5= imfilter ( img 0 , ws ,’circular ‘ ) ;
   Figure ;
   Subplot (2, 3, 1) ;
   Imshow ( img 0 ) ;
   Title ( ‘ Original Image ‘) ;
   Subplot (2, 3,2) ;
   Imshow ( img 1 ) ;
   Title ( ‘ After H Prewitt Filter ‘ ) ;
   Subplot (2, 3,3) ;
   Imshow ( img 2 ) ;
   Title ( ‘ After V Prewitt Filter ‘ ) ;
   Subplot (2, 3,4) ;
   Imshow ( img 3 ) ;
   Title ( ‘ After Mixed HV Prewitt Filter ‘ ) ;
   Subplot (2, 3,5 ) ;
   Imshow ( img 4 ) ;
   Title ( ‘ After H Sobel Filter ‘ ) ;
   Subplot (2, 3,6 ) ;
   Imshow ( img 5 ) ;
   Title ( ‘ After V Sobel Filter ‘ ) ;

دقت وظرافت فیلتر Sobel بیشتر از فیلتر  prewitt میباشد .

فیلتر unsharp موءلفه ای بنام  آلفا دارد .

1. Clc;
   Clear ;
   Close all ;
   Img 0 = imread ( ‘ rice . png ‘ ) ;
   Img 0 = im2double ( img 0 ) ;
   Alpha = 0 ;
   W = fspecial ( ‘unsharp‘ , alpha ) ;
   Img 1= imfilter ( img 0 , w ,’circular ‘ ) ;
   Figure ;
   Subplot (1, 2 , 1) ;
   Imshow ( img 0 ) ;
   Title ( ‘ Original Image ‘) ;
   Subplot (1, 2,2) ;
   Imshow ( img 1 ) ;
   Title ( ‘ After Unsharp Filter ‘ ) ;

 

1. Clc;
   Clear ;
   Close all ;
   Img 0 = imread ( ‘ rice . png ‘ ) ;
   Img 0 = im2double ( img 0 ) ;
   Wp = fspecial ( ‘ prewitt ‘ ) ;
   Img 1= imfilter ( img 0 , wp ,’circular ‘ ) ;
   Img 2= imfilter ( img 0 , wp ,’circular ‘ ) ;
   % Alpha = 0 . 5;
   % img 3 = imfilter ( img 0 , alpha * wp + ( 1 – alpha ) * wp ‘ , ‘ circular ‘ ) ;
   Img 3= sqrt ( img 1 . ^ 2 + img 2 . ^ 2 ) ;
   Ws = fspecial ( ‘ Sobel ‘ ) ;
   Img 4= imfilter ( img 0 , ws ,’circular ‘ ) ;
   Img 5= imfilter ( img 0 , ws ,’circular ‘ ) ;
   Figure ;
   Subplot (2, 3, 1) ;
   Imshow ( img 0 ) ;
   Title ( ‘ Original Image ‘) ;
   Subplot (2, 3,2) ;
   Imshow ( img 1 ) ;
   Title ( ‘ After H Prewitt Filter ‘ ) ;
   Subplot (2, 3,3) ;
   Imshow ( img 2 ) ;
   Title ( ‘ After V Prewitt Filter ‘ ) ;
   Subplot (2, 3,4) ;
   Imshow ( img 3 ) ;
   Title ( ‘ After Mixed HV Prewitt Filter ‘ ) ;
   Subplot (2, 3,5 ) ;
   Imshow ( img 4 ) ;
   Title ( ‘ After H Sobel Filter ‘ ) ;
   Subplot (2, 3,6 ) ;
   Imshow ( img 5 ) ;
   Title ( ‘ After V Sobel Filter ‘ ) ;
   
   

در متلب برای اجرای مستقیم عملیات غیر خطی ماتریسی نداریم ، با ساختن دو فیلتر خطی و حساب کردن  آر اِم اِس آنها میتوانیم این عملیات را اجرا کنیم . فیلتر ترتیبی نمونه مهمی از فیلترهای غیر خطی میباشد .

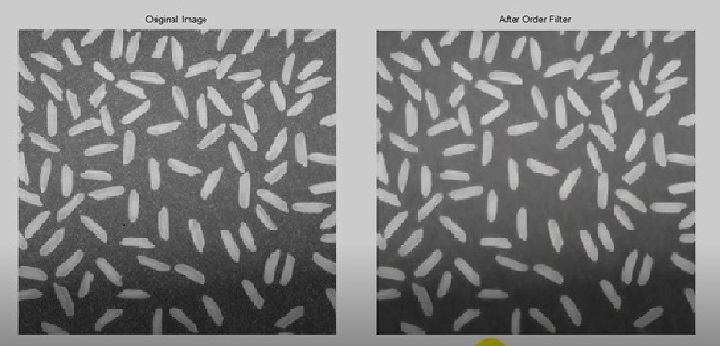
فیلتر ترتیبی مرجع آن روشن ترین نقطه است و از بزرگ به کوچک مرتب میکند در اصلاح تصویر کاربرد دارد و تصاویر را به شکل کاملتری نمایش میدهد .

بررسی کارائی فیلتر ترتیبی Ordfilt 2 :

1. Clc;
   Clear ;
   Close all ;
   Img 0 = imread ( ‘ rice . png ‘ ) ;
   Img 0 = im2double ( img 0 ) ;
   M = 5 ;
   N = 3 ;
   Domain = ones ( M , N ) ;
   Img 1 = ordfilt 2 ( img 0 , M * N , Domain ) ;
   Figure ;
   Subplot ( 1 , 2 , 1 ) ;
   Imshow ( img 0 ) ;
   Title ( ‘ Original Image ‘) ;
   Subplot ( 1 , 2 , 2) ;
   Imshow ( img 1 ) ;
   Title ( ‘ After  Order  Filter ‘ ) ;

عدد بزرگتر ازبین [5  ،  3] قرار میدهیم .

1. Img 1 = ordfilt 2 ( img 0 ,  0 , Domain ) ;

عدد صفر را در دستور تابع Ordfilt 2 میگذاریم صفحه سیاه دستاورد آن است .

1. Img 1 = ordfilt 2 ( img 0 ,  ( M * N + 1 ) / 2 , Domain ) ;

 

با قرار دادن میانه گزینه های تصادفی حذف میشود وتصویر بلوری ارائه میدهد .

میانگین ممکن است زیر مجموعه عضو ها نباشد ولی میانه حتما در عضوها است .

1. Clc;
   Clear ;
   Close all ;
   Img 0 = imread ( ‘ rice . png ‘ ) ;
   Img 0 = im2double ( img 0 ) ;
   M = 5 ;
   N = 3 ;
   Domain = ones ( M , N ) ;
   Img 1 = ordfilt 2 ( img 0 ,( M * N + 1 ) / 2  , Domain ) ;
   Img 2 = imnoise ( img 0 , ‘ salt  &  pepper ‘ ) ;
   Img 3 = ordfilt 2 ( img 2 , ( M * N  + 1 ) / 2 , Domain ) ;
   Figure ;
   Subplot (2 , 2 , 1 ) ;
   Imshow ( img 0 ) ;
   Title ( ‘ Original Image ‘) ;
   Subplot (2, 2 , 2) ;
   Imshow ( img 1 ) ;
   Title ( ‘ After  Order  Filter ‘ ) ;
   Subplot (2 , 2 , 3) ;
   Imshow ( img 2 ) ;
   Title ( ‘ Noisy  Image ‘) ;
   Subplot (2, 2 ,4) ;
   Imshow ( img 3 ) ;
   Title ( ‘Noisy  Image  After  Order  Filter ‘ ) ;

با استفاده از فیلتر نویز را برطرف کردیم .

 

1. M = 5 ;
   N = 5 ;
   Img 1 = Medfilt 2 ( img 0  , [ M N] ) ;
   Img 2 = imnoise ( img 0 , ‘ salt  &  pepper ‘ ) ;
   Img 3 = medfilt 2 ( img 2 , [M N ] ) ;

رسیدن سریع و آسان با تابع  Medfilt 2 .

اسامی نویزها در جدول :

 

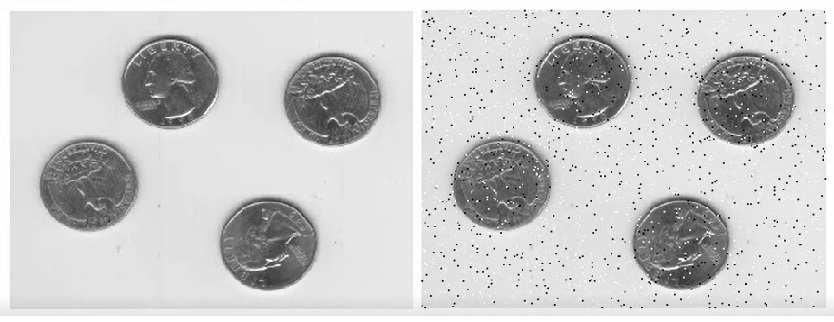
1. I = imread ( ‘ eight . tif ‘ ) ;
   J = imnoise ( I , ‘ salt & pepper ‘ , 0 . 02 ) ;
   Figure , imshow ( I )
   Figure , imshow ( J )
   
   

توابع Log – Laplacian -Ordfilt درنرم افزار متلب در تصویر دارای نویز انواع فرکانس ها موجود است در رنگ ثابت فرکانسی نمیباشد .

ادامه در مبحث 7