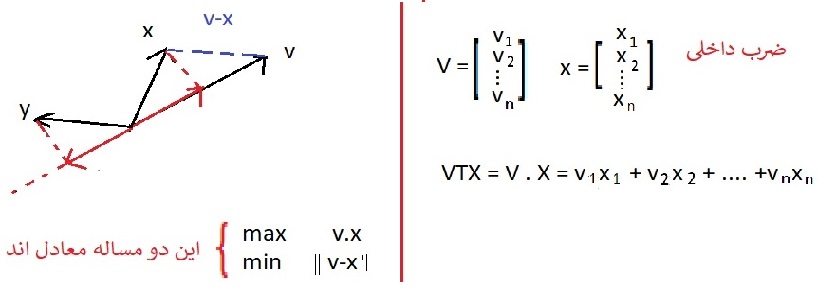تبدیل تابع مکانی به تابع فرکانسی در متلب 

 متریک ها و ماتریس ضرایب فیلتر مکانی در متلب

آموزش برنامه نویسی در متلب 10

 نوشته ها :

1- تبدیل تابع مکانی به تابع فرکانسی 

2-  فیلتر در حوزه فرکانس

3- تابع بر اساس فاصله از مبدا

4- مقایسه فیلتر بالا گذر و پایین گذر

5- با انواع متریک ها آشنا میشویم

6-  آشنایی با ماتریس ضرب داخلی 

7- آشنایی با ماتریس ضرایب  فیلتر مکانی

 تبدیل یک تابع مکانی به یک تابع فرکانسی در متلب :

1- تبدیل مستقیم از fft2 ماتریس مکان و با fft2 تصویر ضرب میکنیم و از حاصل ضربشان معکوس تبدیل فوریه میگیریم .

2- از طریق فیلتر Freqz2  متلب که دقت و سرعت بیشتری از fft2 دارد .

1. Clc ;
   Clear ;
   Close all ;
   f = imread ( ‘ rice . png ‘ ) ;
   f = im2double ( f ) ;
   h = fspecial ( ‘ motion ‘ , 10 , 45 ) ;
   H1 = freqz2 ( h , size ( f , 1 ) , size ( f , 2 ) ) ;
   H = ifftshift ( H1 ) ;
   G = H . * F ;
   g = ifft2 ( G ) ;
   figure ;
   subplot ( 2 , 3 , 1 ) ;
   imshow ( f ) ;
   title ( ‘ Original Image ‘ ) ;
   subplot ( 2 , 3 , 2) ;
   hn = h / max ( h ( : ) ) ;
   imshow (hn) ;
   title ( ‘ The Motion Filter ‘ ) ;
   subplot ( 2 , 3 , 3) ;
   imshow (g ) ;
   title ( ‘ Filtered Image ‘ ) ;
   subplot ( 2 , 3 ,4 ) ;
   imshow (abs ( F ) ) ;
   title ( ‘ Original Image ( FFT ) ‘ ) ;
   subplot ( 2 , 3 , 5 ) ;
   imshow (abs (H) ) ;
   title ( ‘ The Motion Filter (FFT) ‘ ) ;
   subplot ( 2 , 3 ,6 ) ;
   imshow (abs (G) ) ;
   title ( ‘ Filtered Image ( FFT ) ‘ ) ;
   
   

Original Image  * The Motion Filter  =  Filtered Image

1. f = imread ( ‘ rice . png ‘ ) ;
   f = im2double ( f ) ;
   h = fspecial ( ‘ motion ‘ , 30 , 45 ) ;
   H1 = freqz2 ( h , size ( f , 1 ) , size ( f , 2 ) ) ;
   H = ifftshift ( H1 ) ;

فقط با تغییر دادن دامنه تغییرات تصویر را ببینیم :

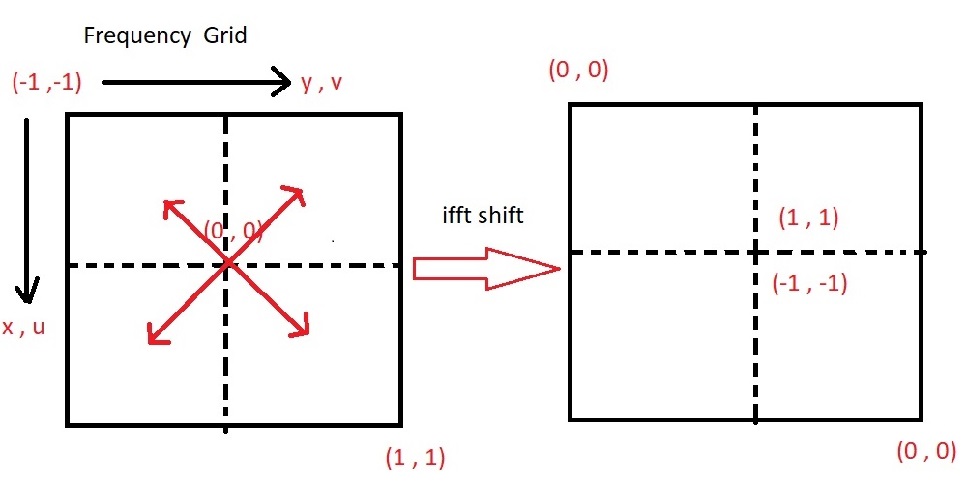
نمایش شکل فیلترهای فرکانسی در حوزه فرکانس :

 

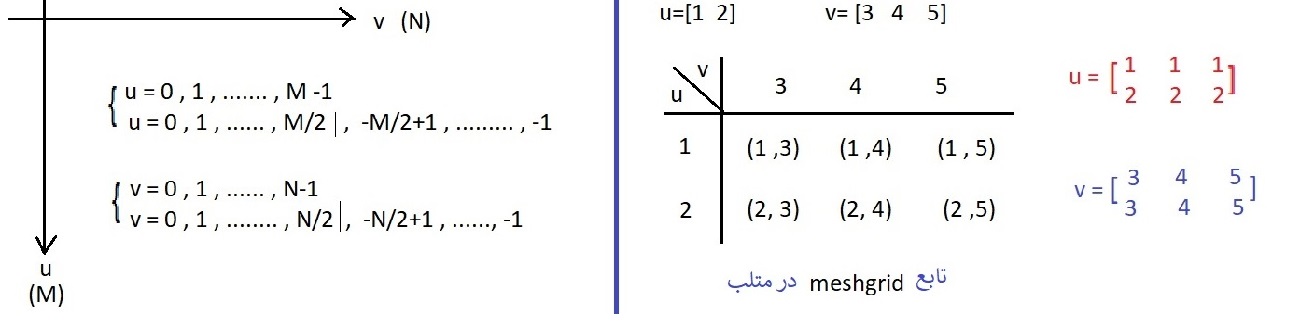
تشکیل شبکه تازه در  u , v  :

1. Function   [u  v] = CreateFreqGrid (M , N)
   U = 0 : M-1 ;
   U( u > M/2 ) = u ( u > M/2 ) – M ;
   V = 0 : N – 1 ;
   V (V > N/2 ) = V ( V > N/2 ) – N ;
   [ U  V ] = meshgrid ( U , V ) ;
   end

کسب پاسخ فرکانسی با جدول فرکانسی

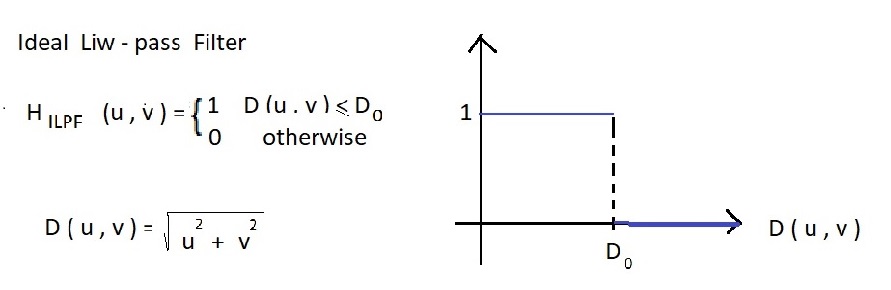
 فیلتر در حوزه فرکانس :

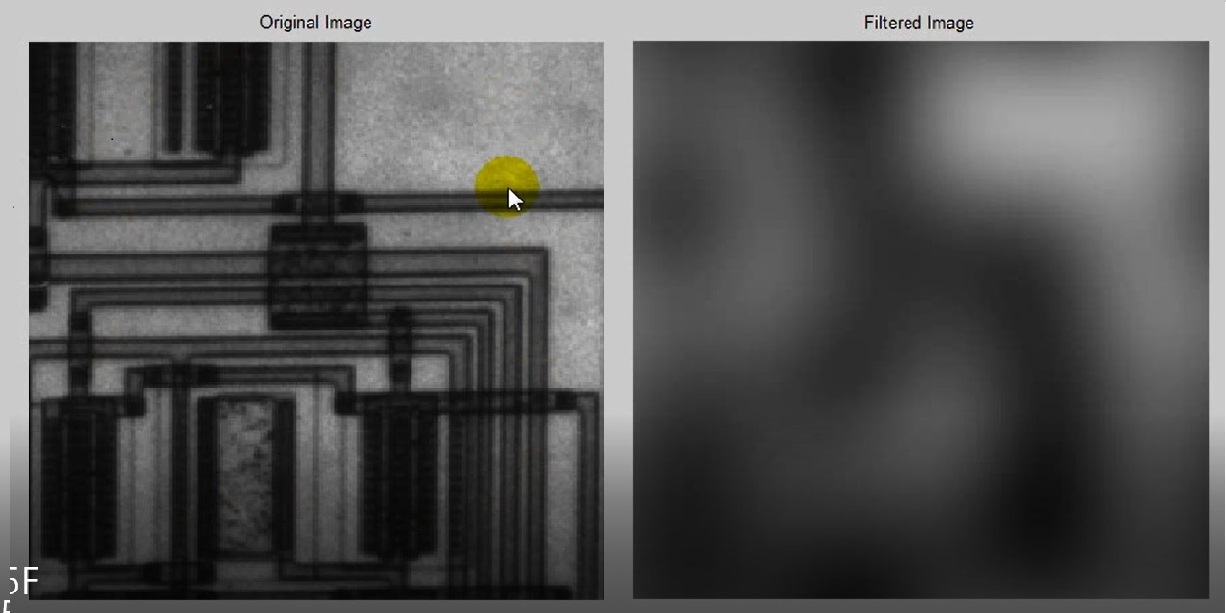
1. Clc ;
   Clear ;
   Close all ;
   % Read Image
   f = imread ( ‘ Circuit . tif ‘ ) ;
   f = im2double ( f ) ;
   F = fft2 (f) ;
   % Define Filter
   d0 = 3 ;
   HLP= @ (d) double ( d< = d0 ) ;
   % Imp Lement Filter
   [ U  V ] = Create Freq Grid ( size ( f , 1 ) , size ( f , 2 ) ) ;
   D = sqrt ( U . ^2 + V . ^2 ) ;
   H = HLP ( D ) ;
   % Apply Filter
   G = H . * F ;
   g= ifft2 ( G ) ;
   % Show Results
   Figure ;
   subplot (1, 2, 1 ) ;
   imshow ( f ) ;
   title ( ‘ Original Image ‘ ) ;
   subplot (1, 2, 2) ;
   imshow (g) ;
   title ( ‘ Filtered Image ‘ ) ;

پهنای باند را اضافه میکنیم میشود :

1. % Define Filter
   d0 = 10 ;
   HLP= @ (d) double ( d< = d0 ) ;

با افزودن پهنای باند وضوح تصویر بیشتر میشود .

تابع را با فاصله از مبدا بررسی میکنیم .

1. Function   [g  G] = Apply Freq Filter (f , HF)
   F = fft2 (f) ;
   [U  V] = Create Freq Grid ( size ( f , 1 ) , size ( f , 2 ) ) ;
   D = Sqrt ( U . ^2 + V. ^2 ) ;
   H = HF ( D ) ;
   G = H . *F ;
   g = ifft2 (G)
   end
   Clc ;
   Clear ;
   Close all ;
   % Read Image
   f = imread ( ‘ Circuit . tif ‘ ) ;
   f = im2double ( f ) ;
   % Define Filter
   d0 = 50 ;
   HLP= @ (d) double ( d< = d0 ) ;
   % Imp Lement Filter
   [g  G] = = Apply Freq Filter (f , HLP) ;
   % Show Results
   Figure ;
   subplot (1, 2, 1 ) ;
   imshow ( f ) ;
   title ( ‘ Original Image ‘ ) ;
   subplot (1, 2, 2) ;
   imshow (g) ;
   title ( ‘ Filtered Image ‘ ) ;
   
   

فاصله از مبدا تابع را خودکار انجام میدهد .

1. Clc ;
   Clear ;
   Close all ;
   % Read Image
   f = imread ( ‘ rice . png ‘ ) ;
   f = im2double ( f ) ;
   % Define Filter
   HLP= @ (d) double ( d< = 20) ;
   HHP= @ (d) double ( d> = 20) ;
   HBP= @ (d) double ( d> =10  &  d< = 30 ) ;
   % Imp Lement Filter
   [g1  G1] = Apply Freq Filter ( f , HLP ) ;
   [g2  G2] = Apply Freq Filter ( f , HHP ) ;
   [g3  G3] = Apply Freq Filter ( f , HBP ) ;
   % Adjust Results
   g1 = imadjust ( g1 ) ;
   g2 = imadjust ( g2 ) ;
   g3 = imadjust ( g3 ) ;
   % Show Results
   Figure ;
   subplot (2, 2, 1 ) ;
   imshow ( f ) ;
   title ( ‘ Original Image ‘ )
   subplot (2, 2, 2) ;
   imshow (g1) ;
   title ( ‘ LOW – Pass Filter ‘ ) ;
   subplot (2, 2,3) ;
   imshow (g2) ;
   title ( ‘ High – Pass Filter ‘ ) ;
   subplot (2, 2,4) ;
   imshow (g3) ;
   title ( ‘Band – Pass Filter ‘ ) ;
   
   

فیلتر پایین گذر تصویر را تار میکند .

از این قابلیتها برای طراحی سیستمهای پلاک خوان و اتوماسیون پارکینگ و همچنین نرم افزار پارکینگ استفاده میشود.

فیلتر بالا گذر حواشی و تغییرات رنگ را بهتر نمایان میکند .

 

1. % Read Image
   f = imread ( ‘ rice . png ‘ ) ;
   f = im2double ( f ) ;
   f = f ( 1 : 64 , 1 : 64 ) ;
   % Define Filters
   norder = 1 ;
   d0 = 5 ;
   w = 5 ;
   HLP= @ (d) 1 . / ( 1 + ( d ./d0 ) . ^(2*norder ) ) ;
   HHP= @ (d) 1 . / ( 1 + ( d ./d0 ) . ^(2*norder ) ) ;
   HBP= @ (d) 1 . / ( 1 + ( ( d . ^2 – d0 ^2) . / (w* d ) ) . ^ ( 2 * norder )

عبور دادن بخشی از اطلاعات تصویر تصاویر متفاوتی حاصل میکند .

پهنای باند در فیلتر میان گذر تصاویر خاصی را نمایش میدهد .

با تغییر فیلترها تصاویر و رفتارهای متنوعی به دست میاوریم .

انواع متریک ها :

 متریک ضرایب مکانی در متلب برای یافتن نواحی تکرار شده تصویر کارایی دارد .

بردار را از روی تصویر میسازیم هر بردار با خودش بیشترین مطابقت را دارد .

تطابق دو بردار از نظر ریاضی :

بهترین وسیله توصیف مقایسه و شباهت  دو بردار ضرب داخلی است که مستقل از اسکیل است .

کار ماتریس ضرایب فیلتر مکانی در متلب تشخیص و شناسایی ضریب وزنی است .

بررسی نقطه های روشن در تصویر g  میزان سیملارتی راتشخیص میدهیم .

 چند نمونه مثال :

 

1. >> im show ( ‘ text . png ‘ )
   >> f = imread ( ‘ text . png ‘ )
   >> a = f ( 32:45 , 88:98 ) ;
   >> imshow (a)
   
   

 

1. Clc ;
   Clear ;
   Close all ;
   f= imread ( ‘ text . png ‘ ) ;
   f= im2double ( f ) ;
   a= f ( 32:45 , 88:98 ) ;
   g= imfilter ( f , a , ‘ circular ‘ ) ;
   figure ;
   subplot ( 2 , 2 , 1 )
   imshow ( f ) ;
   title ( ‘ Original Image ‘ ) ;
   subplot ( 2 , 2 , 2)
   imshow ( a ) ;
   title ( ‘ The pattern ‘ ) ;
   subplot ( 2 , 2 , 3)
   imshow ( g ) ;
   title ( ‘Filtered Image ‘ ) ;
   
   

1. Clc ;
   Clear ;
   Close all ;
   f= imread ( ‘ text . png ‘ ) ;
   f= im2double ( f ) ;
   a= f ( 32:45 , 88:98 ) ;
   a = a/sum ( a ( : ) ) ;
   g= imfilter ( f , a , ‘ circular ‘ ) ;
   g max = max ( g (:) ) ;
   th = 60 ;
   g2 = double ( g > = th ) ;
   g = g /max ( g ( : ) ) ;
   h = fspecial ( ‘ average ‘ , 7 ) ;
   g3 = imfilter ( g2 , h ) ;
   g3 = double ( g3 > 0 ) ;
   figure ;
   subplot ( 2 , 2 , 1 )
   imshow ( f ) ;
   title ( ‘ Original Image ‘ ) ;
   subplot ( 2 , 2 , 2)
   imshow ( a ) ;
   title ( ‘ The pattern ‘ ) ;
   subplot ( 2 , 2 , 3)
   imshow ( g ) ;
   title ( ‘Filtered Image ‘ ) ;
   subplot ( 2 , 2 ,4)
   imshow ( g2 ) ;
   title ( ‘ Processed Image ‘ ) ;
   
   

1. Clc ;
   Clear ;
   Close all ;
   f= imread ( ‘ text . png ‘ ) ;
   f= im2double ( f ) ;
   F = fft2 ( f ) ;
   a0 = f ( 32:45 , 88:98 ) ;
   A0 = fft2 (a0 , size ( f , 1 ) , size ( f , 2 ) ) ;
   a1 = rot 90 (a0 , 1 ) ;
   A1 = fft2 (a1 , size ( f , 1 ) , size ( f , 2 ) ) ;
   a2 = rot 90 (a0 , 2) ;
   A2 = fft2 (a2 , size ( f , 1 ) , size ( f , 2 ) ) ;
   a3 = rot 90 (a0 , 3) ;
   A3 = fft2 (a3 , size ( f , 1 ) , size ( f , 2 ) ) ;
   G0 = A0 . * F ;
   g0 = real (ifft2 ( G0 ) ) ;
   G1 = A1 . * F ;
   g1 = real (ifft2 ( G1 ) ) ;
   G2 = A2 . * F ;
    g2 = real (ifft2 ( G2 ) ) ;
   G3 = A3 . * F ;
   g3 = real (ifft2 ( G3 ) ) ;
   g = g0 ;
   g = max ( g , g1 )
   g = max ( g , g2 )
   g = max ( g , g3 )
   th = 60 ;
   g2 = double ( g > = th ) ;
   g = g / max ( g ( : ) ) ;
   h = fspecial ( ‘ average ‘ , 7 ) ;
   g3 = imfilter ( g2 , h ) ;
   g3 = double ( g3 > 0 ) ;
   figure ;
   subplot ( 2 , 2 , 1 )
   imshow ( f ) ;
   title ( ‘ Original Image ‘ ) ;
   subplot ( 2 , 2 , 2)
   imshow ( a0 ) ;
   title ( ‘ The pattern ‘ ) ;
   subplot ( 2 , 2 , 3)
   imshow ( g ) ;
   title ( ‘Filtered Image ‘ ) ;
   subplot ( 2 , 2 ,4)
   imshow ( g3 ) ;
   title ( ‘ Processed Image ‘ ) ;
   
   

شناسایی 3 تصویر a  در افق و عمود .

1. Clc ;
   Clear ;
   Close all ;
   f= imread ( ‘ text . png ‘ ) ;
   G3 = A3 . * F ;
   g3 = real (ifft2 ( G3 ) ) ;
   g = g0 ;
   g = max ( g , g1 )
   g = max ( g , g2 )
   g = max ( g , g3 )
   th = 60 ;
   h= double ( g > = th ) ;
   for           i= 1 : size ( h , 1 )
        for       j = 1 : size ( h , 2 )
               if       h ( i, j ) = 1
                            h ( (i– 13 ) : i, ( j – 10 ) : j ) = 1 ;
   end
   figure ;
   subplot ( 2 , 2 , 1 )
   imshow ( f ) ;
   title ( ‘ Original Image ‘ ) ;
   subplot ( 2 , 2 , 2)
   imshow ( a0 ) ;
   title ( ‘ The pattern ‘ ) ;
   subplot ( 2 , 2 , 3)
   imshow ( g ) ;
   title ( ‘Filtered Image ‘ ) ;
   subplot ( 2 , 2 ,4)
   imshow (h) ;
   title ( ‘ Processed Image ‘ ) ;
   figure ;
   RGB ( : , : , 1 ) = double (Xor ( f , h ) ) ;
   RGB ( : , : , 2) = f ;
   RGB ( : , : , 3) = f ;
   Imsh0w ( RGB ) ;
   
   

اجرا شدن کُریلیشن در حوزه های فیلتری مکان و فرکانس .

فیلتر کُریلیشن الگوهای ثابت را در تصویر شناسایی میکند اما در برابر عواملی مثل نویز و دوران های غیر صحیح و بزرگ و کوچک شدن مقاوم نیست .

اساس تشخیص در متلب ضرب داخلی است .

ادامه در مبحث 11